I’ve noticed more and more papers using the phrase “comprehensive model”. This phrase grates every time, and this post is about why.
I thought this might just be me getting old and grumpy, so I plotted the mentions of the phrases “comprehensive mathematical model” or “comprehensive model” in ‘Topic’ in Web of Science over the years in Figure 1. Sure enough, more papers in recent years feature models that are comprehensive*.
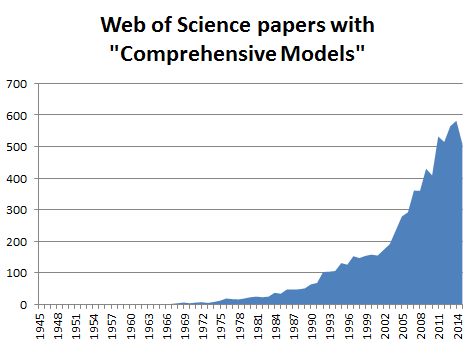
Figure 1: the rise of Comprehensive Models! Mentions of “Comprehensive Models” or “Comprehensive Mathematical Models” in Web of Science 1945 – 2015.
So why don’t I think a mathematical model is ever comprehensive?
Usually by comprehensive the authors mean something like this describes most of what we’ve seen well enough to say/predict something (or even to within the observational error bounds in some physics experiments). Perhaps their model integrates information/theories that weren’t part of a single conceptual framework/mathematical model before. That’s great – but it isn’t comprehensive!
This post is really an excuse to plug and discuss the following quotation from James Black (physiologist and Nobel Prize winner for developing the first beta-blockers). He summarises what mathematical models are and aren’t, and what they are for, beautifully:
[Mathematical] models in analytical pharmacology are not meant to be descriptions, pathetic descriptions, of nature; they are designed to be accurate descriptions of our pathetic thinking about nature. They are meant to expose assumptions, define expectations and help us to devise new tests.
Sir James Black (1924 – 2010)
Nobel Prize Lecture, 1988**
A mathematical model isn’t supposed to be a comprehensive representation of a system – it’s always going to be a pathetic representation in many ways! Models make simplifying assumptions (by definition***), generally ignoring things that we think will make a smaller difference to the model’s predictions than the things that we have included (usually things that happen really fast/slow or that are really small/big).
What models do allow us to do is see exactly what we would expect to happen if the system works in the simple(ish!) way we think it does. Then that can teach us loads about whether the system does work as we thought it did, or whether something fundamental is missing from our understanding.
We’ll always be able to come back and add more detail as time goes on, we learn more, and can measure more things. So that means that a model is never finished, and never comprehensive. So I’d say let’s avoid using the word comprehensive to describe any kind of model!
A Large Confession: I thought the word comprehensive implied ‘includes everything’. Purely to back up my point I looked it up, and sure enough one of the OED’s definitions is “grasps or understands (a thing) fully” which a model never does; but another is “having the attribute of comprising or including much; of large content or scope” which might be OK! Hmmmm… given the ambiguity I still conclude we’d better avoid the word anyway! But I’ll let you make your own minds up:
